Classification of red vs white wines
Goal
Build a classifier that differentiates between red and white whines based on chemical properties.
Data Collection
Same as previous post
Data Engineering
Combined the red wine and white wine csv files into a single data frame and added a target feature, color, to indicate what type of wine the example was:
redWines = pd.read_csv('winequality-red.csv', delimiter=";")
whiteWines = pd.read_csv('winequality-white.csv', delimiter=";")
redWines = redWines.drop(columns=['quality'])
whiteWines = whiteWines.drop(columns=['quality'])
redWines['color'] = 1
whiteWines['color'] = 0
wines = redWines.append(whiteWines)
wines = wines.reset_index(drop=True)
Stored the target variable separately and performed mean normalization:
wineType = wines['color']
wines = np.stack(wines.drop(columns=['color']).values)
wines=(wines-wines.mean())/wines.std()
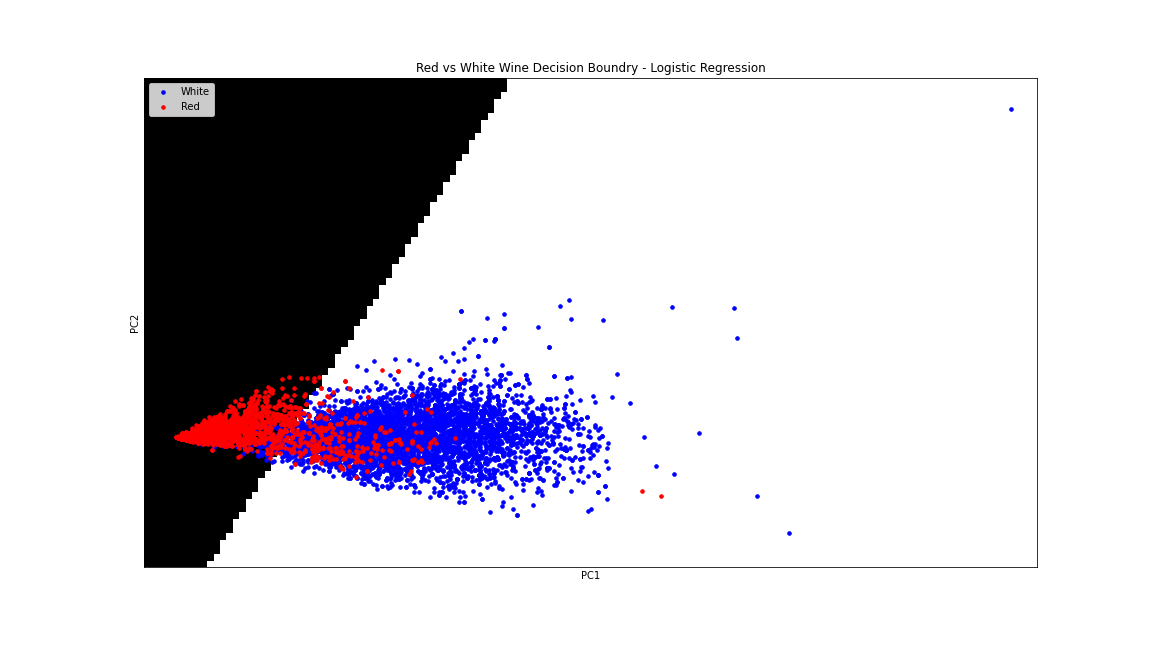
For data visualization purposes used Principle Component Analysis to reduce dimensionality to 2 components. The images won’t 100% indicate what the model was trained on and how it classifies though.
Results
Logistic Regression
X_train, X_valid, y_train, y_valid = train_test_split(wines, wineType, test_size=0.2)
model = make_pipeline(
LogisticRegression(C=1e3,max_iter=250)
)
model.fit(X_train, y_train)
print(model.score(X_train, y_train))
print(model.score(X_valid, y_valid))
0.985
0.98
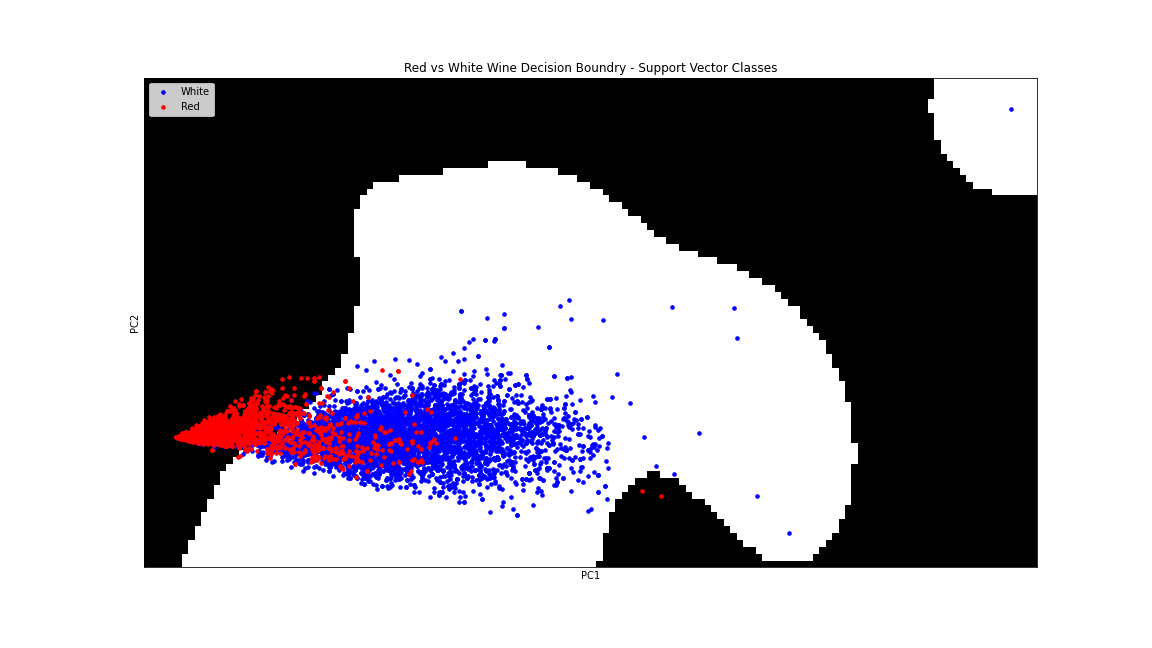
Support Vector Classes
X_train, X_valid, y_train, y_valid = train_test_split(wines, wineType, test_size=0.25)
model = make_pipeline(
SVC(C=10000)
)
model.fit(X_train, y_train)
print(model.score(X_train, y_train))
print(model.score(X_valid, y_valid))
0.991
0.988
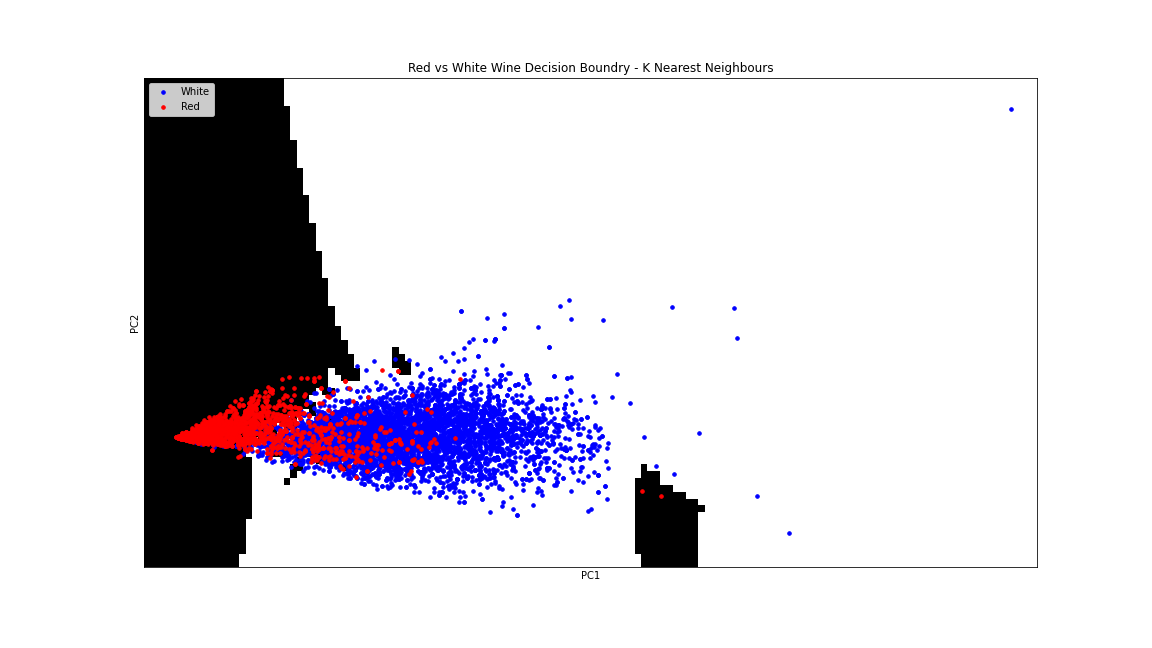
K Nearest Neighbours
X_train, X_valid, y_train, y_valid = train_test_split(wines, wineType, test_size=0.25)
model = make_pipeline(
KNeighborsClassifier(n_neighbors=3)
)
model.fit(X_train, y_train)
print(model.score(X_train, y_train))
print(model.score(X_valid, y_valid))
0.968
0.942
Conclusion
Both SVC and Logistic regression required a very high regularization parameter to get the scores they did. With C=1 both were around the low to mid 90’s. So there’s some question on whether they’re overfitting and if they’d generalize well to new data points.